2021年二建水利通關藍寶書
2021年二建市政通關藍寶書在線閱讀
2022考蟲數學高數必練1000題pdf
黃岡歷年中考物理試卷及答案解析2007-2020年整合版
黃岡市中考化學試卷2012-2020年整合版
黃岡中考英語試卷及答案2007-2020整合word版
計算機畢業設計:ASP語言設計完整版
2021年中國95后女性洞察報告pdf免費在線閱讀
中國減貧學報告電子版免費在線閱讀
幼兒園綜合素質學習筆記pdf電子版
編輯點評：包含了從2011年到2020年歷年中考試卷和答案
黃岡的中考試題相對來說參考價值還是比較大的，黃岡數學中考試卷及答案2011-2020年整合版包含了黃岡10年以來的試卷試題和答案解析，高清的doc文檔格式，可以編輯沒有水印，直接打印用來復習非常不錯。
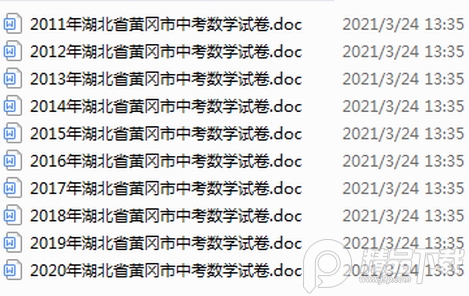
黃岡歷年中考數學試題圖片預覽
目錄大全
2011年湖北省黃岡市中考數學試卷.doc
2012年湖北省黃岡市中考數學試卷.doc
2013年湖北省黃岡市中考數學試卷.doc
2014年湖北省黃岡市中考數學試卷.doc
2015年湖北省董岡市中考數學試卷.doc
2016年湖北省黃岡市中考數學試卷.doc
2017年湖北省黃岡市中考數學試卷.doc
2018年湖北省黃岡市中考數學試卷.doc
2019年湖北省黃岡市中考數學試卷.doc
2020年湖北省黃岡市中考數學試卷.doc
試題及答案預覽
2020年湖北省黃岡市中考數學試卷
一、選擇題（本題共8小題，每小題3分，共24分．每小題給出的4個選項中，有且只有一個答案是正確的）
1．（3分）的相反數是（ ）
A．B．﹣6C．6D．﹣
2．（3分）下列運算正確的是（ ）
A．m+2m＝3m2B．2m3?3m2＝6m6
C．（2m）3＝8m3D．m6÷m2＝m3
3．（3分）已知一個正多邊形的一個外角為36°，則這個正多邊形的邊數是（ ）
A．7B．8C．9D．10
4．（3分）甲、乙、丙、丁四位同學五次數學測驗成績統計如下表所示，如果從這四位同學中，選出一位同學參加數學競賽．那么應選（ ）去．
甲乙丙丁
平均分85909085
方差50425042
A．甲B．乙C．丙D．丁
5．（3分）下列幾何體是由4個相同的小正方體搭成的，其中，主視圖、左視圖、俯視圖都相同的是（ ）
A．B．
C．D．
6．（3分）在平面直角坐標系中，若點A（a，﹣b）在第三象限，則點B（﹣ab，b）所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
7．（3分）若菱形的周長為16，高為2，則菱形兩鄰角的度數之比為（ ）
A．4：1B．5：1C．6：1D．7：1
8．（3分）2020年初以來，紅星消毒液公司生產的消毒液在庫存量為m噸的情況下，日銷售量與產量持平．自1月底抗擊“新冠病毒”以來，消毒液需求量猛增，該廠在生產能力不變的情況下，消毒液一度脫銷，下面表示2020年初至脫銷期間，該廠庫存量y（噸）與時間t（天）之間函數關系的大致圖象是（ ）
A．B．
C．D．
二、填空題（本題共8小題，每小題3分，共24分）
9．（3分）計算＝ ．
10．（3分）已知x1，x2是一元二次方程x2﹣2x﹣1＝0的兩根，則＝ ．
11．（3分）若|x﹣2|+＝0，則﹣xy＝ ．
12．（3分）已知：如圖，在△ABC中，點D在邊BC上，AB＝AD＝DC，∠C＝35°，則∠BAD＝ 度．
13．（3分）計算：÷（1﹣）的結果是 ．
14．（3分）已知：如圖，AB∥EF，∠ABC＝75°，∠CDF＝135°，則∠BCD＝ 度．
15．（3分）我國古代數學著作《九章算術》中有這樣一個問題：”今有池方一丈，葭（jiā）生其中央，出水一尺．引葭赴岸，適與岸齊．問水深幾何？”（注：丈，尺是長度單位，1丈＝10尺）這段話翻譯成現代漢語，即為：如圖，有一個水池，水面是一個邊長為1丈的正方形，在水池正中央有一根蘆葦，它高出水面1尺．如果把這根蘆葦拉向水池一邊的中點，它的頂端恰好到達池邊的水面，則水池里水的深度是 尺．
16．（3分）系統找不到該試題
三、解答題（本題共9題，滿分72分）
17．（5分）解不等式x+≥x，并在數軸上表示其解集．
18．（6分）已知：如圖，在?ABCD中，點O是CD的中點，連接AO并延長，交BC的延長線于點E，求證：AD＝CE．
19．（6分）為推廣黃岡各縣市名優農產品，市政府組織創辦了“黃岡地標館”，一顧客在“黃岡地標館”發現，如果購買6盒羊角春牌綠茶和4盒九孔牌藕粉，共需960元，如果購買1盒羊角春牌綠茶和3盒九孔牌藕粉共需300元，請問每盒羊角春牌綠茶和每盒九孔牌藕粉分別需要多少元？
20．（7分）為了解疫情期間學生網絡學習的學習效果，東坡中學隨機抽取了部分學生進行調查．要求每位學生從“優秀”，“良好”，“一般”，“不合格”四個等次中，選擇一項作為自我評價網絡學習的效果．現將調查結果繪制成如圖兩幅不完整的統計圖，請結合圖中所給的信息解答下列問題：
（1）這次活動共抽查了 人．
（2）將條形統計圖補充完整，并計算出扇形統計圖中，學習效果“一般”的學生人數所在扇形的圓心角度數．
（3）張老師在班上隨機抽取了4名學生，其中學習效果“優秀”的1人，“良好”的2人，“一般”的1人，若再從這4人中隨機抽取2人，請用畫樹狀圖法，求出抽取的2人學習效果全是“良好”的概率．
21．（7分）已知：如圖，AB是⊙O的直徑，點E為⊙O上一點，點D是上一點，連接AE并延長至點C，使∠CBE＝∠BDE，BD與AE交于點F．
（1）求證：BC是⊙O的切線；
（2）若BD平分∠ABE，求證：AD2＝DF?DB．
22．（8分）因東坡文化遠近聞名的遺愛湖公園，“國慶黃金周”期間，游人絡繹不絕，現有一艘游船載著游客在遺愛湖中游覽，當船在A處時，船上游客發現岸上P1處的臨摹亭和P2處的遺愛亭都在東北方向，當游船向正東方向行駛600m到達B處時，游客發現遺愛亭在北偏西15°方向，當游船繼續向正東方向行駛400m到達C處時，游客發現臨摹亭在北偏西60°方向．
（1）求A處到臨摹亭P1處的距離；
（2）求臨摹亭P1處與遺愛亭P2處之間的距離．（計算結果保留根號）
23．（8分）已知：如圖，一次函數的圖象與反比例函數的圖象交于A，B兩點，與y軸正半軸交于點C，與x軸負半軸交于點D，OB＝，tan∠DOB＝．
（1）求反比例函數的解析式；
（2）當S△ACO＝S△OCD時，求點C的坐標．
24．（11分）網絡銷售已經成為一種熱門的銷售方式，為了減少農產品的庫存，我市市長親自在某網絡平臺上進行直播銷售大別山牌板栗，為提高大家購買的積極性，直播時，板栗公司每天拿出2000元現金，作為紅包發給購買者．已知該板栗的成本價格為6元/kg，每日銷售量y（kg）與銷售單價x（元/kg）滿足關系式：y＝﹣100x+5000．經銷售發現，銷售單價不低于成本價且不高于30元/kg．當每日銷售量不低于4000kg時，每千克成本將降低1元，設板栗公司銷售該板栗的日獲利為w（元）．
（1）請求出日獲利w與銷售單價x之間的函數關系式；
（2）當銷售單價定為多少時，銷售這種板栗日獲利最大？最大利潤為多少元？
（3）當w≥40000元時，網絡平臺將向板栗公司收取a元/kg（a＜4）的相關費用，若此時日獲利的最大值為42100元，求a的值．
25．（14分）已知拋物線y＝ax2+bx+c與x軸交于點A（﹣1，0），點B（3，0），與y鈾交于點C（0，3）．頂點為點D．
（1）求拋物線的解析式；
（2）若過點C的直線交線段AB于點E，且S△ACE：S△CEB＝3：5，求直線CE的解析式；
（3）若點P在拋物線上，點Q在x軸上，當以點D，C，P，Q為頂點的四邊形是平行四邊形時，求點P的坐標；
（4）已知點H（0，），G（2，0），在拋物線對稱軸上找一點F，使HF+AF的值最小．此時，在拋物線上是否存在一點K，使KF+KG的值最小？若存在，求出點K的坐標；若不存在，請說明理由．
2020年湖北省黃岡市中考數學試卷
參考答案與試題解析
一、選擇題（本題共8小題，每小題3分，共24分．每小題給出的4個選項中，有且只有一個答案是正確的）
1．【分析】只有符號不同的兩個數是互為相反數，在數軸上表示，分別位于原點的兩側，且到原點距離相等的兩點所表示的數是互為相反數．
【解答】解：的相反數是﹣，
故選：D．
【點評】本題考查相反數的意義和求法，理解相反數的意義是正確解答的前提．
2．【分析】利用合并同類項、同底數冪的乘除法以及冪的乘方、積的乘方進行計算即可．
【解答】解：m+2m＝3m，因此選項A不符合題意；
2m3?3m2＝6m5，因此選項B不符合題意；
（2m）3＝23?m3＝8m3，因此選項C符合題意；
m6÷m2＝m6﹣2＝m4，因此選項D不符合題意；
故選：C．
【點評】本題考查合并同類項的法則、同底數冪的乘除法以及冪的乘方、積的乘方的計算方法，掌握計算法則是得出正確答案的前提．
3．【分析】利用多邊形的外角和是360°，正多邊形的每個外角都是36°，即可求出答案．
【解答】解：360°÷36°＝10，所以這個正多邊形是正十邊形．
故選：D．
【點評】本題主要考查了多邊形的外角和定理．是需要識記的內容．
4．【分析】先找到四人中平均數大的，即成績好的；再從平均成績好的人中選擇方差小，即成績穩定的，從而得出答案．
【解答】解：∵＝＞＝，
∴四位同學中乙、丙的平均成績較好，
又＜，
∴乙的成績比丙的成績更加穩定，
綜上，乙的成績好且穩定，
故選：B．
【點評】本題主要考查方差，解題的關鍵是掌握方差的意義：方差是反映一組數據的波動大小的一個量．方差越大，則平均值的離散程度越大，穩定性也越小；反之，則它與其平均值的離散程度越小，穩定性越好．
5．【分析】根據主視圖是從物體的正面看得到的視圖，俯視圖是從上面看得到的圖形，左視圖是左邊看得到的圖形，可得答案．
【解答】解：A．主視圖、左視圖、俯視圖均為底層是兩個小正方形，上層的左邊是一個小正方形，故本選項符合題意；
B主視圖與左視圖均為底層是兩個小正方形，上層的左邊是一個小正方形；而俯視圖的底層左邊是一個小正方形，上層是兩個小正方形，故本選項不合題意；
C．主視圖與俯視圖均為一行三個小正方形，而左視圖是一列兩個小正方形，故本選項不合題意．
D．主視圖為底層兩個小正方形，上層的右邊是一個小正方形；左視圖為底層是兩個小正方形，上層的左邊是一個小正方形；俯視圖的底層左邊是一個小正方形，上層是兩個小正方形，故本選項不合題意；
故選：A．
【點評】本題考查了簡單組合體的三視圖，利用三視圖的意義是解題關鍵．
6．【分析】根據點A（a，﹣b）在第三象限，可得a＜0，﹣b＜0，得b＞0，﹣ab＞0，進而可以判斷點B（﹣ab，b）所在的象限．
【解答】解：∵點A（a，﹣b）在第三象限，
∴a＜0，﹣b＜0，
∴b＞0，
∴﹣ab＞0，
∴點B（﹣ab，b）所在的象限是第一象限．
故選：A．
【點評】本題考查了點的坐標，解決本題的關鍵是掌握點的坐標特征．
7．【分析】如圖，AH為菱形ABCD的高，AH＝2，利用菱形的性質得到AB＝4，利用正弦的定義得到∠B＝30°，則∠C＝150°，從而得到∠C：∠B的比值．
【解答】解：如圖，AH為菱形ABCD的高，AH＝2，
∵菱形的周長為16，
∴AB＝4，
在Rt△ABH中，sinB＝＝＝，
∴∠B＝30°，
∵AB∥CD，
∴∠C＝150°，
∴∠C：∠B＝5：1．
故選：B．
【點評】本題考查了菱形的性質：菱形具有平行四邊形的一切性質；菱形的四條邊都相等；菱形的兩條對角線互相垂直，并且每一條對角線平分一組對角．也考查了直角三角形斜邊上的中線性質．
8．【分析】根據開始產量與銷量持平，后來脫銷即可確定存量y（噸）與時間t（天）之間函數關系．
【解答】解：根據題意：時間t與庫存量y之間函數關系的圖象為先平，再逐漸減小，最后為0．
故選：D．
【點評】本題要求能夠通過圖象得到函數是隨自變量的增大，知道函數值是增大還是減小，通過圖象得到函數是隨自變量的增大或減小的快慢．
二、填空題（本題共8小題，每小題3分，共24分）
9．【分析】依據立方根的定義求解即可．
【解答】解：＝﹣2．
故答案為：﹣2．
【點評】本題主要考查的是立方根的性質，熟練掌握立方根的性質是解題的關鍵．
10．【分析】根據x1，x2是方程x2+px+q＝0的兩根時x1x2＝q，得出x1x2＝﹣1，代入計算可得答案．
【解答】解：∵x1，x2是一元二次方程x2﹣2x﹣1＝0的兩根，
∴x1x2＝﹣1，
則＝﹣1，
故答案為：﹣1．
【點評】本題主要考查根與系數的關系，解題的關鍵是掌握x1，x2是方程x2+px+q＝0的兩根時，x1+x2＝﹣p，x1x2＝q．
11．【分析】根據非負數的性質進行解答即可．
【解答】解：∵|x﹣2|+＝0，
∴x﹣2＝0，x+y＝0，
∴x＝2，y＝﹣2，
∴，
故答案為2．
【點評】本題考查了非負數的性質，掌握幾個非負數的和為0，這幾個數都為0，是解題的關鍵．
12．【分析】根據等腰三角形的性質和三角形的內角和定理即可得到結論．
【解答】解：∵AD＝DC，
∴∠DAC＝∠C＝35°，
∴∠ADB＝∠DAC+∠C＝70°．
∵AB＝AD，
∴∠B＝∠ADB＝70°，
∴∠BAD＝180°﹣∠B﹣∠ADB＝180°﹣70°﹣70°＝40°．
故答案為：40．
【點評】本題考查了等腰三角形的性質及三角形內角和為180°等知識．此類已知三角形邊之間的關系求角的度數的題，一般是利用等腰（等邊）三角形的性質得出有關角的度數，進而求出所求角的度數．
13．【分析】先計算括號內分式的減法、將被除式分母因式分解，再將除法轉化為乘法，最后約分即可得．
【解答】解：原式＝÷（﹣）
＝÷
＝?
＝，
故答案為：．
【點評】本題主要考查分式的混合運算，解題的關鍵是掌握分式的混合運算順序和運算法則．
14．【分析】根據鄰補角的定義得到∠EDC＝180°﹣135°＝45°，根據平行線的性質得到∠1＝∠ABC＝75°，根據三角形外角的性質即可得到結論．
【解答】解：∵∠CDF＝135°，
∴∠EDC＝180°﹣135°＝45°，
∵AB∥EF，∠ABC＝75°，
∴∠1＝∠ABC＝75°，
∴∠BCD＝∠1﹣∠EDC＝75°﹣45°＝30°，
故答案為：30．
【點評】本題考查了平行線的性質，三角形外角的性質，鄰補角的定義，熟練掌握平行線的性質是解題的關鍵．
15．【分析】根據勾股定理列出方程，解方程即可．
【解答】解：設水池里水的深度是x尺，
由題意得，x2+52＝（x+1）2，
解得：x＝12，
答：水池里水的深度是12尺．
故答案為：12．
【點評】本題考查的是勾股定理的應用，掌握勾股定理、根據勾股定理正確列出方程是解題的關鍵．
16．
三、解答題（本題共9題，滿分72分）
17．【分析】去分母、移項、合并、系數化為1即可得到不等式的解集為x≥﹣3，然后在數軸上表示解集即可．
【解答】解：去分母得4x+3≥3x，
移項、合并得x≥﹣3，
所以不等式的解集為x≥﹣3，
在數軸上表示為：
【點評】本題考查了解一元一次不等式，掌握解法的基本步驟：去分母，去括號，移項，合并同類項，系數化為1是解題的關鍵．
18．【分析】只要證明△AOD≌△EOC（ASA）即可解決問題；
【解答】證明：∵O是CD的中點，
∴OD＝CO，
∵四邊形ABCD是平行四邊形，
∴AD∥BC，
∴∠D＝∠OCE，
在△ADO和△ECO中，
，
∴△AOD≌△EOC（ASA），
∴AD＝CE．
【點評】此題主要考查了全等三角形的判定與性質，平行四邊形的性質等知識，解題的關鍵是正確尋找全等三角形解決問題．
19．【分析】設每盒羊角春牌綠茶需要x元，每盒九孔牌藕粉需要y元，根據“如果購買6盒羊角春牌綠茶和4盒九孔牌藕粉，共需960元，如果購買1盒羊角春牌綠茶和3盒九孔牌藕粉共需300元”，即可得出關于x，y的二元一次方程組，解之即可得出結論．
【解答】解：設每盒羊角春牌綠茶需要x元，每盒九孔牌藕粉需要y元，
依題意，得：，
解得：．
答：每盒羊角春牌綠茶需要120元，每盒九孔牌藕粉需要60元．
【點評】本題考查了二元一次方程組的應用，找準等量關系，正確列出二元一次方程組是解題的關鍵．
20．【分析】（1）由“良好”的人數及其所占百分比可得總人數；
（2）求出“不合格”的學生人數為20人，從而補全條形統計圖；由360°乘以學習效果“一般”的學生人數所占的百分比即可；
（3）畫出樹狀圖，利用概率公式求解即可．
【解答】解：（1）這次活動共抽查的學生人數為80÷40%＝200（人）；
故答案為：200；
（2）“不合格”的學生人數為200﹣40﹣80﹣60＝20（人），
將條形統計圖補充完整如圖：
學習效果“一般”的學生人數所在扇形的圓心角度數為360°×＝108°；
（3）把學習效果“優秀”的記為A，“良好”記為B，“一般”的記為C，
畫樹狀圖如圖：
共有12個等可能的結果，抽取的2人學習效果全是“良好”的結果有2個，
∴抽取的2人學習效果全是“良好”的概率＝＝．
【點評】本題考查了列表法或畫樹狀圖法、概率公式以及條形統計圖和扇形統計圖的有關知識．列表法或畫樹狀圖法可以不重復不遺漏的列出所有可能的結果，列表法適合于兩步完成的事件，樹狀圖法適合兩步或兩步以上完成的事件．注意概率＝所求情況數與總情況數之比．
21．【分析】（1）根據圓周角定理即可得出∠EAB+∠EBA＝90°，再由已知得出∠ABE+∠CBE＝90°，則CB⊥AB，從而證得BC是⊙O的切線；
（2）通過證得△ADF∽△BDA，得出相似三角形的對應邊成比例即可證得結論．
【解答】證明：（1）∵AB是⊙O的直徑，
∴∠AEB＝90°，
∴∠EAB+∠EBA＝90°，
∵∠CBE＝∠BDE，∠BDE＝∠EAB，
∴∠EAB＝∠CBE，
∴∠EBA+∠CBE＝90°，即∠ABC＝90°，
∴CB⊥AB，
∵AB是⊙O的直徑，
∴BC是⊙O的切線；
（2）證明：∵BD平分∠ABE，
∴∠ABD＝∠DBE，
∵∠DAF＝∠DBE，
∴∠DAF＝∠ABD，
∵∠ADB＝∠ADF，
∴△ADF∽△BDA，
∴，
∴AD2＝DF?DB．
【點評】本題考查了切線的判定，三角形相似的判定和性質；要證某線是圓的切線，已知此線過圓上某點，連接圓心與這點（即為半徑），再證垂直即可．
22．【分析】（1）如圖，作P1M⊥AC于M，設P1M＝x，在兩個直角三角形中，利用三角函數即可x表示出AM與CM，根據AC＝AM+CM即可列方程，從而求得P1M的長，進一步求得AP1的長；
（2）作BN⊥AP2于N，在兩個直角三角形中，利用三角函數即可求出AN與P2N，根據（1）的結果求得P1N，從而求得P1P2．
【解答】解：（1）作P1M⊥AC于M，
設P1M＝x，
在Rt△P1AM中，∵∠P1AB＝45°，
∴AM＝P1M＝x，
在Rt△P1CM中，∵∠P1CA＝30°，
∴MC＝＝x，
∵AC＝1000，
∴x+＝1000，解得x＝500（﹣1），
∴P1M＝500（﹣1）m
∴P1A＝＝500（﹣）m，
故A處到臨摹亭P1處的距離為500（﹣）m；
（2）作BN⊥AP2于N，
∵∠P2AB＝45°，∠P2BA＝75°，
∴∠P2＝60°，
在Rt△ABN中，∵∠P1AB＝45°，AB＝600m
∴BN＝AN＝AB＝300，
∴P1N＝500（﹣）﹣300＝500﹣800，
在Rt△P2BN中，∵∠P2＝60°，
∴P2N＝BN＝×＝100，
∴P1P2＝100﹣（500﹣800）＝800﹣400．
故臨摹亭P1處與遺愛亭P2處之間的距離是（800﹣400）m．
【點評】本題主要考查了直角三角形的計算，一般的三角形可以通過作高線轉化為解直角三角形的計算，計算時首先計算直角三角形的公共邊是常用的思路．
23．【分析】（1）根據OB＝，tan∠DOB＝，可求出點B的坐標，進而確定反比例函數的關系式；
（2）利用S△ACO＝S△OCD，可得OD＝2AN，再根據相似三角形的性質，設AN＝a、CN＝b，表示出OD、OC，最后根據三角形OBM的面積為|k|＝1，列方程求出b的值即可．
【解答】解：過點B、A作BM⊥x軸，AN⊥x軸，垂足為點M，N，
（1）在Rt△BOM中，OB＝，tan∠DOB＝．
∵BM＝1，OM＝2，
∴點B（﹣2，﹣1），
∴k＝（﹣2）×（﹣1）＝2，
∴反比例函數的關系式為y＝；
（2）∵S△ACO＝S△OCD，
∴OD＝2AN，
又∵△ANC∽△DOC，
∴＝＝＝，
設AN＝a，CN＝b，則OD＝2a，OC＝2b，
∵S△OAN＝|k|＝1＝ON?AN＝×3b×a，
∴ab＝，①，
由△BMD∽△CNA得，
∴＝，即＝，也就是a＝②，
由①②可求得b＝1，b＝﹣（舍去），
∴OC＝2b＝2，
∴點C（0，2）．
【點評】本題考查反比例函數、一次函數圖象上點的坐標特征，理解反比例函數k的幾何意義是列方程的關鍵．
24．【分析】（1）分兩種情況討論，由日獲利＝銷售單價×數量，可求解；
（2）分兩種情況討論，由二次函數的性質，分別求出6≤x≤10和10＜x≤30時的最大利潤，即可求解；
（3）由w≥40000元，可得w與x的關系式為w＝﹣100x2+5600x﹣32000，可求當20≤x≤36時，w≥40000，可得日獲利w1＝（x﹣6﹣a）（﹣100x+5000）﹣2000＝﹣100x2+（5600+100a）x﹣32000﹣5000a，由二次函數的性質可求解．
【解答】解：（1）當y≥4000，即﹣100x+5000≥4000，
∴x≤10，
∴當6≤x≤10時，w＝（x﹣6+1）（﹣100x+5000）﹣2000＝﹣100x2+5500x﹣27000，
當10＜x≤30時，w＝（x﹣6）（﹣100x+5000）﹣2000＝﹣100x2+5600x﹣32000，
綜上所述：w＝；
（2）當6≤x≤10時，w＝﹣100x2+5500x﹣27000＝﹣100（x﹣）2+48625，
∵a＝﹣100＜0，對稱軸為x＝，
∴當6≤x≤10時，y隨x的增大而增大，即當x＝10時，w最大值＝18000元，
當10＜x≤30時，w＝﹣100x2+5600x﹣32000＝﹣100（x﹣28）2+46400，
∵a＝﹣100＜0，對稱軸為x＝28，
∴當x＝28時，w有最大值為46400元，
∵46400＞18000，
∴當銷售單價定為28時，銷售這種板栗日獲利最大，最大利潤為46400元；
（3）∵40000＞18000，
∴10＜x≤30，
∴w＝﹣100x2+5600x﹣32000，
當w＝40000元時，40000＝﹣100x2+5600x﹣32000，
∴x1＝20，x2＝36，
∴當20≤x≤36時，w≥40000，
又∵10＜x≤30，
∴20≤x≤30，
此時：日獲利w1＝（x﹣6﹣a）（﹣100x+5000）﹣2000＝﹣100x2+（5600+100a）x﹣32000﹣5000a，
∴對稱軸為直線x＝＝28+a，
∵a＜4，
∴28+a＜30，
∴當x＝28+a時，日獲利的最大值為42100元
∴（28+a﹣6﹣a）[﹣100×（28+a）+500]﹣2000＝42100，
∴a1＝2，a2＝86，
∵a＜4，
∴a＝2．
【點評】本題考查了二次函數的應用，二次函數的性質，利用分類討論思想解決問題是本題的關鍵．
25．【分析】（1）因為拋物線經過A（﹣1，0），B（3，0），可以假設拋物線的解析式為y＝a（x+1）（x﹣3），利用待定系數法解決問題即可．
（2）求出點E的坐標即可解決問題．
（3）分點P在x軸的上方或下方，點P的縱坐標為1或﹣1，利用待定系數法求解即可．
（4）如圖3中，連接BH交對稱軸于F，連接AF，此時AF+FH的值最小．求出直線HB的解析式，可得點F的坐標，設K（x，y），作直線y＝，過點K作KM⊥直線y＝于M．證明KF＝KM，利用垂線段最短解決問題即可．
【解答】解：（1）因為拋物線經過A（﹣1，0），B（3，0），
∴可以假設拋物線的解析式為y＝a（x+1）（x﹣3），
把C（0，3）代入，可得a＝﹣1，
∴拋物線的解析式為y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3．
（2）如圖1中，連接AC，BC．
∵S△ACE：S△CEB＝3：5，
∴AE：EB＝3：5，
∵AB＝4，
∴AE＝4×＝，
∴OE＝0.5，
設直線CE的解析式為y＝kx+b，則有，
解得，
∴直線EC的解析式為y＝﹣6x+3．
（3）由題意C（0，3），D（1，4）．
當四邊形P1Q1CD，四邊形P2Q2CD是平行四邊形時，點P的縱坐標為1，
當y＝1時，﹣x2+2x+3＝1，
解得x＝1±，
∴P1（1+，1），P2（1﹣，1），
當四邊形P3Q3DC，四邊形P4Q4DC是平行四邊形時，點P的縱坐標為﹣1，
當y＝﹣1時，﹣x2+2x+3＝﹣1，
解得x＝1±，
∴P1（1+，﹣1），P2（1﹣，﹣1），
綜上所述，滿足條件的點P的坐標為（1+，1）或（1﹣，1）或（1﹣，﹣1）或（1+，﹣1）．
（4）如圖3中，連接BH交對稱軸于F，連接AF，此時AF+FH的值最小．
∵H（0，），B（3，0），
∴直線BH的解析式為y＝﹣x+，
∵x＝1時，y＝，
∴F（1，），
設K（x，y），作直線y＝，過點K作KM⊥直線y＝于M．
∵KF＝，y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴（x﹣1）2＝4﹣y，
∴KF＝＝＝|y﹣|，
∵KM＝|y﹣|，
∴KF＝KM，
∴KG+KF＝KG+KM，
根據垂線段最短可知，當G，K，M共線，且垂直直線y＝時，GK+KM的值最小，最小值為，
此時K（2，3）．
【點評】本題屬于二次函數綜合題，考查了待定系數法，一次函數的性質，平行四邊形的判定和性質，垂線段最短等知識，解題的關鍵是學會用分類討論的思想思考問題，第四個問題的關鍵是學會用轉化的思想思考問題，把最短問題轉化為垂線段最短，屬于中考壓軸題．
聲明：試題解析著作權屬菁優網所有，未經書面同意，不得復制發布
黃岡歷年中考試題及答案解析2012-2020年語文試卷word無水印版
幼兒園保教知識與能力學習筆記pdf電子版免費版
小學教育教學知識與能力學習筆記電子版手寫板
中學綜合素質學習筆記在線閱讀完整版
中學教育知識與能力學習筆記pdf電子版免費版
專插本英語詞匯必備3400pdf完整版
廣東省專插本必刷2000題政治理論答案電子版免費版
2020全國中考物理真題及答案解析合集免費版
2020全國中考英語真題試卷及答案解析整合版
2020全國中考數學真題試卷及答案解析匯總大全docx可打印版
2020全國中考語文真題及解析匯總整合版免費版docx完整版
數學物理方程講義完整版1-5講電子版pdf高清無水印版
2021各科中考總復習專題知識要點pdf整合版
大小： 32.7M
中考復習資料大全
新高考復習資料合集
三年級復習資料合集
二級建造師考試資料大全
數學題庫文檔
十二校聯合教育學基礎第三版筆記和課后習題pdf免費版
2021新高考數學一輪復習真題和模擬題匯編pdf免費下載
支持( 0 ) 蓋樓(回復)