欢迎您访问【千度】vh969.com-永久免费毛片在线播放,亚洲深夜在线,影音先锋最新av资源库,歪歪漫画登录官方入口页面弹窗

2021年新高考數學名校地市必刷題合集word版新高考專用版 全站導航最近更新

  • 戰壕戰爭1914國際版(Trench Warfare1914) 像素風策略戰爭游戲
  • 網易光遇手游正版 點亮星空共慶周年
  • 地鐵跑酷體驗服國際服all stars 地鐵跑酷體驗服版本
  • 六花軟件庫app手機安卓吧 超多軟件各種版本資源隨意下載。
  • 李跳跳自動跳廣告MissLee 幫你自動跳廣告
歷史搜索

熱門搜索：冒險島楓之傳說手游黎明覺醒生機騰訊正版攜程旅行app手機版地鐵跑酷手游國服逃跑吧少年官方版

首頁 → 教程素材 → 教程資料 → 2021年新高考數學名校地市必刷題合集word版 新高考專用版
2021年新高考數學名校地市必刷題合集word版圖標

2021年新高考數學名校地市必刷題合集word版新高考專用版

  • 大小：5.5M
  • 時間：2021-01-11 14:50
  • 星級：
  • 語言：中文
  • 環境：WinAll
  • 版本：新高考專用版
  • 類別：國產軟件/ 免費軟件
  • 官網：暫無
  • 廠商：

軟件介紹 軟件截圖 相關下載 相關文章 評論(0)

精品下載精心為您推薦：

編輯點評：包含了18個文檔

專門為2021年新高考整理的一份名校地市必刷題包含了9個專題，有集合運算，真假命題判斷與應用，函數，導數，不等式，數列等等，題題有新意,讓你在好題中析情境、練方法、提能力、拔成績!

2021年新高考數學名校地市必刷題合集word版

2021年新高考數學名校地市必刷題電子版預覽

目錄介紹

專題01集合運算-2021年新高考數學名校地市必刷題（新高考專用）

專題02真假命題判斷與應用-2021年新高考數學名校地市必刷題（新高考專用）

專題03函數-2021年新高考數學名校地市必刷題（新高考專用）

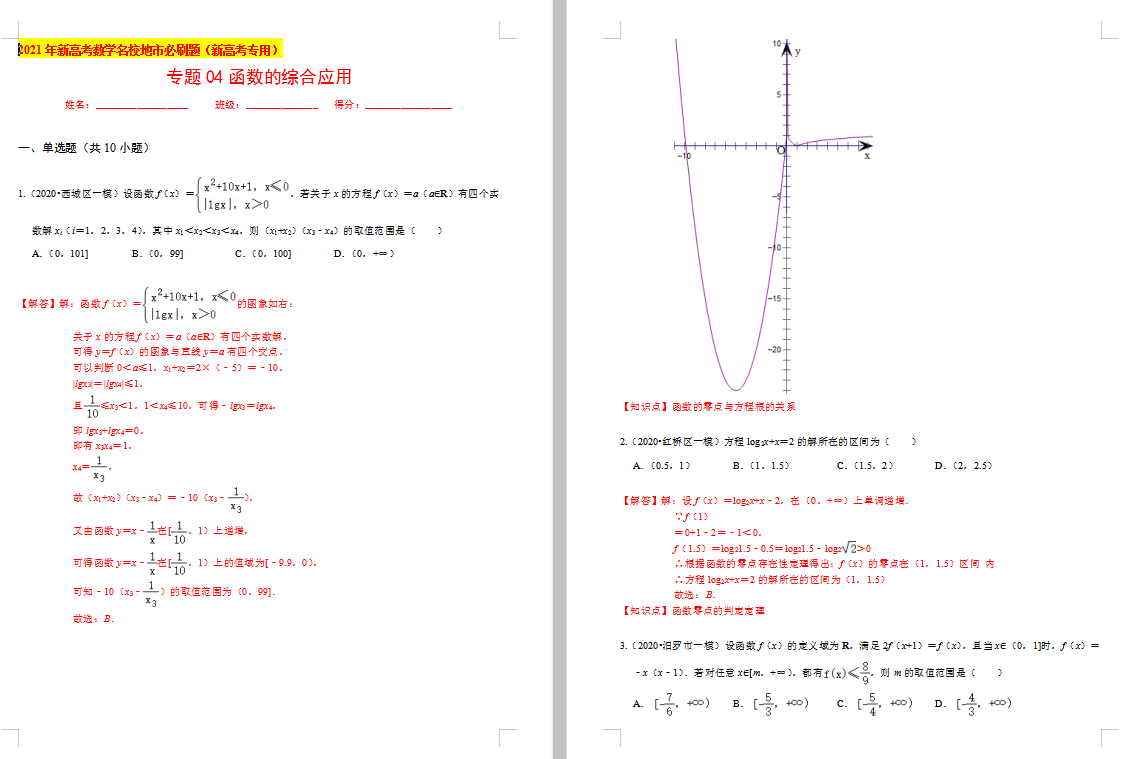
專題04函數的綜合應用-2021年新高考數學名校地市必刷題（新高考專用）

專題05導數-2021年新高考數學名校地市必刷題（新高考專用）

專題06不等式-2021年新高考數學名校地市必刷題（新高考專用）

專題07數列-2021年新高考數學名校地市必刷題（新高考專用）

專題08平面向量-2021年新高考數學名校地市必刷題（新高考專用）

專題09排列組合與概率統計-2021年新高考數學名校地市必刷題（新高考專用）

詳細內容

專題01集合運算-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題01集合運算-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題02真假命題判斷與應用-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題02真假命題判斷與應用-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題03函數-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題03函數-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題04函數的綜合應用-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題04函數的綜合應用-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題05導數-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題05導數-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題06不等式-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題06不等式-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題07數列-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題07數列-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題08平面向量-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題08平面向量-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

專題09排列組合與概率統計-2021年新高考數學名校地市必刷題（新高考專用）（解析版）.docx

專題09排列組合與概率統計-2021年新高考數學名校地市必刷題（新高考專用）（原卷版）.docx

試題預覽

一、單選題（共10小題）

1.（2018?安徽模擬）刪去正整數數列1，2，3，…中的所有完全平方數，得到一個新數列，這個數列的第2018項是（　　）

A．2062B．2063C．2064D．2065

2.（2019?定遠縣三模）已知數列{an}的前n項和為Sn，，且a2＝a9，則所有滿足條件的數列中，a1的最大值為（　　）

A．3B．6C．9D．12

3.（2019?烏魯木齊模擬）已知等差數列{an}的公差不為零，且a2，a3，a9成等比數列，則＝（　　）

A．B．C．D．

4.（2019?青島二模）中國歷法推測遵循以測為輔、以算為主的原則．例如《周髀算經》和《易經》里對二十四節氣的晷（guǐ）影長的記錄中，冬至和夏至的晷影長是實測得到的，其它節氣的晷影長則是按照等差數列的規律計算得出的．如表為《周髀算經》對二十四節氣晷影長的記錄，其中115.1寸表示115寸1分（1寸＝10分）．

已知《易經》中記錄的冬至晷影長為130.0寸，春分晷影長為72.4寸，那么《易經》中所記錄的夏至的晷影長應為（　　）

A．14.8寸B．15.8寸C．16.0寸D．18.4寸

5.（2020?岳陽一模）已知{an}為等差數列，a3＝52，a1+a4+a7＝147，{an}的前n項和為Sn，則使得Sn達到最大值時n是（　　）

A．19B．20C．39D．40

6.（2019?新疆模擬）已知等比數列{an}的各項均為正數，且log3a1+log3a2+…+log3a9＝9，則a3a7+a4a6＝（　　）

A．6B．9C．18D．81

7.（2019?青島三模）已知{an}為等比數列，a10，a30是方程x2﹣11x+16＝0的兩實根，則a20等于（　　）

A．3B．±4C．4D．±3

8.（2019?上海模擬）已知等比數列{an}的首項為2，公比為﹣，其前n項和記為Sn，若對任意的n∈N*，均有A≤3Sn﹣≤B恒成立，則B﹣A的最小值為（　　）

A．B．C．D．

9.（2019?江西模擬）已知數列{an}的通項公式是，其中的部分圖象如圖所示，Sn為數列{an}的前n項和，則S2019的值為（　　）

A．﹣1B．0C．D．1

10.（2018?邵陽三模）在△ABC中，||＝||＝4，＝8，平面ABC內一點P滿足＝2+3，若||＝2，則的最大值為（　　）

A．18B．21C．24D．26

19.（2019?西湖區校級模擬）已知a∈R，函數f（x）＝log2[（a﹣3）x+3a﹣4]．

（1）當a＝2時，解不等式f（3x）＜0；

（2）若函數y＝f（x2﹣4x）的值域為R，求實數a的取值范圍；

（3）設，若函數y＝g（x）有且只有一個零點，求實數a的取值范圍．

20.（2018?新華區校級模擬）已知函數f（x）＝（x3﹣6x2+3x+t）ex，t∈R．

（1）若函數y＝f（x）依次在x＝a，x＝b，x＝c（a＜b＜c）處取到極值．

①求t的取值范圍；

②若a+c＝2b2，求t的值．

（2）若存在實數t∈[0，2]，使對任意的x∈[1，m]，不等式f（x）≤x恒成立．求正整數m的最大值．

21.（2020?肇慶三模）設函數f（x）＝|x﹣a|+|x+b|，ab＞0．

（1）當a＝1，b＝1時，求不等式f（x）＜3的解集；

（2）若f（x）的最小值為2，求的最小值．

22.（2019?重慶模擬）已知函數f（x）＝|x﹣1|+|x+a|，

（1）當a＝﹣2時，求不等式f（x）＜g（x）的解集；

（2）若a＞﹣1，且當x∈[﹣a，1]時，不等式f（x）≤g（x）有解，求實數a的取值范圍．

23.（2019?西湖區校級模擬）解關于x的不等式（x﹣2）（ax﹣2）＞0．

24.（2019?岳陽二模）岳陽市某高中文學社計劃招入女生x人，男生y人，若x，y滿足約束條件，則該社團今年計劃招入學生人數最多為　　　．

2021年新高考數學名校地市必刷題合集word版截圖

下載地址

    網友評論

    熱門評論

    最新評論

    發表評論查看所有評論(0)

    昵稱:
    表情: 高興 可 汗 我不要 害羞 好 送花 親親
    字數: 0/500 (您的評論需要經過審核才能顯示)

    TOP榜

    日韩一二三区| 久久精品国产亚洲AV成人| 免费国产美女爽到喷出水来视频|