国产精品第1页在线观看_亚洲人午夜射精精品日韩_秋霞网在线伦理免费

欢迎您访问【千度】vh969.com-永久免费毛片在线播放,亚洲深夜在线,影音先锋最新av资源库,歪歪漫画登录官方入口页面弹窗

高斯課堂概率論與數理統計及答案pdf免費版全站導航最近更新

戰壕戰爭1914國際版(Trench Warfare1914) 像素風策略戰爭游戲
網易光遇手游正版點亮星空共慶周年
地鐵跑酷體驗服國際服all stars 地鐵跑酷體驗服版本
六花軟件庫app手機安卓吧超多軟件各種版本資源隨意下載。
李跳跳自動跳廣告MissLee 幫你自動跳廣告

歷史搜索

首頁 → 教程素材 → 教程資料 → 高斯課堂概率論與數理統計及答案pdf免費版

高斯課堂概率論與數理統計及答案pdf免費版

大小：1021KB

時間：2020-11-11 10:49

星級：

語言：中文

環境：WinAll

版本：

類別：國產軟件/ 免費軟件

官網：暫無

廠商：

軟件介紹軟件截圖相關下載相關文章評論(0)

精品下載精心為您推薦：

編輯點評：

讓你4小時速成不掛科的蜂考高斯課堂的概率論與數理統計所配套的講義，精品下載站附上最新高清無水印的高斯課堂概率論與數理統計及答案pdf免費下載，包含了14課時內容，需要的自己拿走不謝。

高斯課堂概率論與數理統計講義預覽

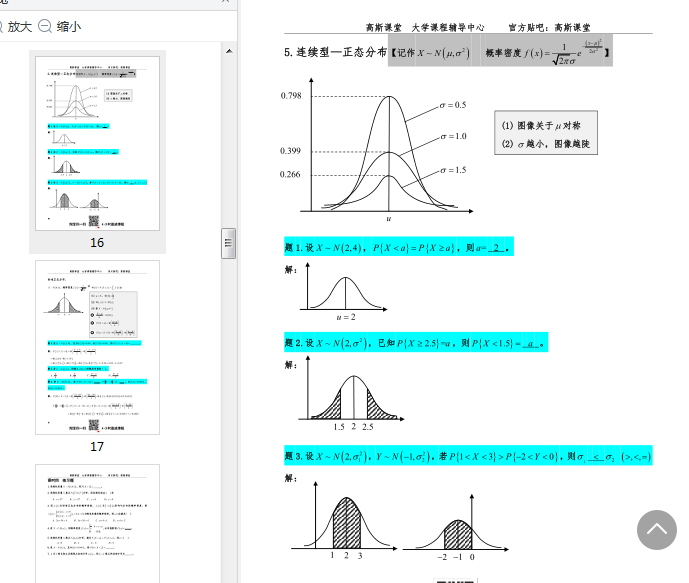
高斯課堂概率論與數理統計及答案pdf免費版

課程大綱

事件運算及概率

全概率、貝葉斯公式

一維隨機變量

五種重要分布

二維離散型隨機變量

二維連續型隨機變量

E維連續型函數的分布

數學期望、方差、協方差

大數定理、中心極限定理

抽樣分布

參數估計

置信區間

假設檢驗

二重積分（選學）

概率論與數理統計答案如下圖

高斯課堂概率論與數理統計及答案pdf免費版

概率論與數理統計學習筆記分享

p1 緒論

p2 樣本空間和隨機事件

隨機試驗

在同樣條件下重復進行

知道所有試驗可能出現的結果

在實驗室不知道這次會出現哪個結果

樣本空間（集合）

隨機試驗所有可能的結果。

隨機事件

樣本空間的子集。
幾個特殊的隨機事件：

必然事件：一定會發生的事假。（比如把整個樣本空間看做一個隨機事件）

不可能事件：空集

基本事件：只包含一個樣本點
例如：公交站現在有多少個人在等車？
樣本空間：S={x : x>=0}
事件A表示等車人數大于等于0 A={x : x>=0} （必然事件）
事件A表示等車人數大于等于5 B={x : x>=5} (隨機事件）
事件C表示恰好有三人等車 C={3} （基本事件）
事件D等車人數多于3且小于3 D={} （不可能事件）

p3 事件的相互關系和運算

關系

包含 A ⊂ B A\subset BA⊂B

相等 A=B

運算

和事件 A ∪ B A\cup BA∪B

積事件 A ∩ B A\cap BA∩B

逆事件A ￣ \overline AA

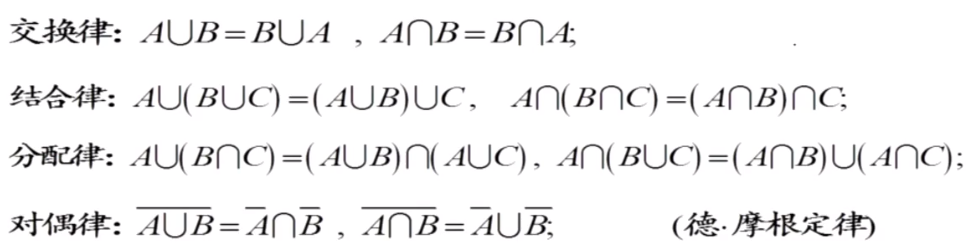
p4頻率

隨機事件A在N次隨機實驗中發生次數所占的比例，隨著N增大趨于穩定。最終穩定到隨機事件A發生的概率。

p5概率

講到概率的的性質和一些簡單的計算公式。

p6古典概型（等可能概型）

樣本空間的樣本點有限（有限性）

每個樣本點出現概率相等（等可能性）

p7條件概率的定義

P ( B ∣ A ) P(B|A)P(B∣A) : A發生的情況下B發生的概率
P ( B ∣ A ) = P ( B A ) P ( A ) P(B|A)= \frac {P(BA)} {P(A)}P(B∣A)=P(A)P(BA)
后面包含了一些經典例題

p8條件概率

經典例題

p9全概率和貝葉斯公式

劃分

樣本空間S
第i事件A即為A i A_iAi
劃分滿足以下性質：

A 1 ∪ A 2 ∪ A 3 ∪ . . . . A n = S A_1\cup A_2\cup A_3 \cup....A_n=SA1∪A2∪A3∪....An=S

任意j,k滿足A j ∩ A k = ϕ A_j \cap A_k=\phiAj∩Ak=ϕ

全概率公式

貝葉斯

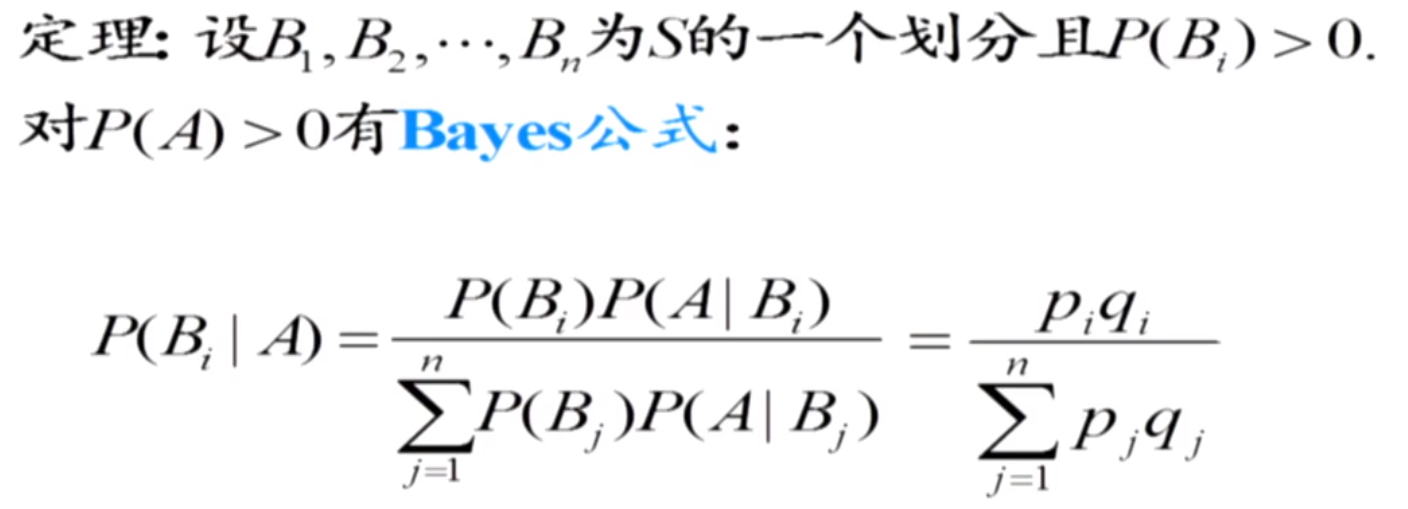
p10全概率和貝葉斯公式

例題講解

p11事件的獨立性

P ( A , B ) = P ( A ) ∗ P ( B ) P(A,B)=P(A)*P(B)P(A,B)=P(A)∗P(B)
獨立和不相容兩個概念，不相同。
獨立性考慮的是A,B會不會相互影響
相容考慮的是兩個事件有無交集

p12事件的獨立性

經典例題

p13隨機變量

隨機變量實際上是一個函數：一個將樣本點映射到實數空間的函數。方便我們描述隨機數事件。

p14隨機變量

分布

所有隨機變量取值及其對應概率

p15離散隨機變量的分布

二項分布（0-1分布）

二項分布記為：
X ～ 0 − 1 ( p ) X\sim 0-1(p)X～0−1(p) 發生概率為p
也可記為X ～ B ( 1 , p ) X\sim B(1,p)X～B(1,p) 也可表示進行一次伯努利實驗，發生的概率為p
X ～ B ( n , p ) X\sim B(n,p)X～B(n,p)表示進行n次伯努利實驗，發生的概率為p
例：拋一枚不均勻的硬幣，正面向上概率為0.4
用X表示拋9次硬幣正面向上的次數：
X服從二項分布X ～ B （ 9 ， 0.4 ） X \sim B（9，0.4）X～B（9，0.4）
用X表示拋9次硬幣正面向上的次數：
X服從二項分布X ～ B （ 9 ， 0.6 ） X \sim B（9，0.6）X～B（9，0.6）
二項分布概率計算方法P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k)=C_n^k p^k{(1-p)}^{n-k}P(X=k)=Cnkpk(1−p)n−k

p16離散隨機變量的分布

泊松分布

X ～ π ( λ ) 或 X ～ P ( λ ) X \sim \pi(\lambda) 或 X \sim P(\lambda)X～π(λ)或X～P(λ)
概率計算公式：
P ( x = k ) = λ k e − λ k ! P(x=k)=\frac{\lambda ^ke^{- \lambda}}{k!}P(x=k)=k!λke−λ

當n>10,p<0.1時泊松分布可看做二項分布的近似。概率計算結果基本一致。

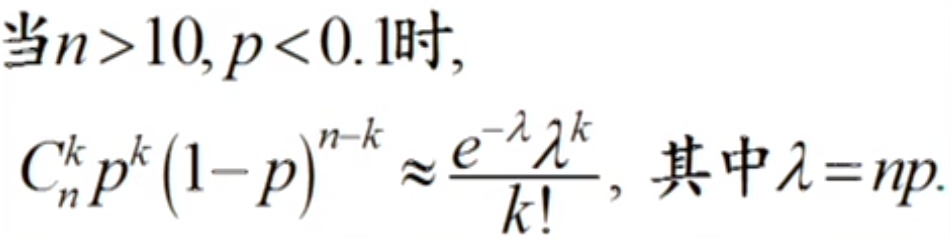
幾何分布

幾何分布記為：
x ～ G e o m ( p ) x \sim Geom(p)x～Geom(p)
概率計算公式：
P ( X = k ) = p ( 1 − p ) k − 1 P(X=k)=p{(1-p)}^{k-1}P(X=k)=p(1−p)k−1
典型服從幾何分布例子：
我們投擲一枚骰子，6點向上時停止投擲。投擲的次數服從幾何分布。

p17分布函數

（可以用來描述連續型和離散型隨機變量的分布）
分布函數
F ( x ) = P （ X ≤ x ）有時記作： F X ( x ) = P （ X ≤ x ） F(x)=P（X\leq x）有時記作：F_X(x)=P（X\leq x）F(x)=P（X≤x）有時記作：FX(x)=P（X≤x）

p18分布函數

離散型隨機變量分布和分布函數互推的例子

p19分布函數

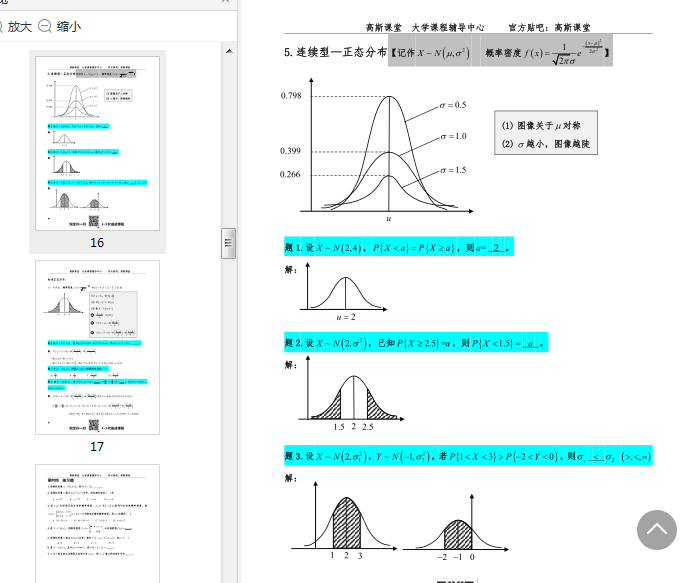
連續性隨機變量的分布函數

p20 連續性隨機概率密度函數

連續性變量才有概率密度函數